01
构图设计的原则
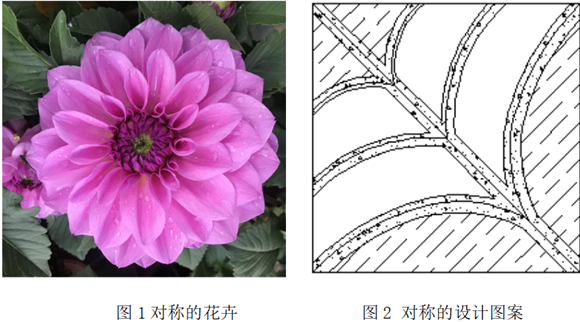
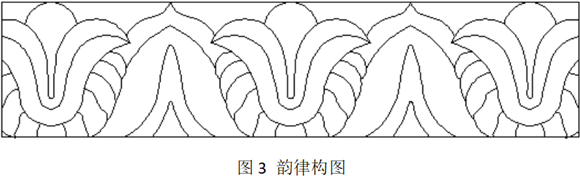
1.1对称美
对称均衡是数学形式美的主要特征,因此对称美是人类利用的最多的数学原理,是自然界中最为普遍的现象。小到分子、原子、大到各种摩天高楼,都是对称美的体现,对称美在自然界无处不在,无时不有,没有对称美的世界是一个不可以想象的世界。
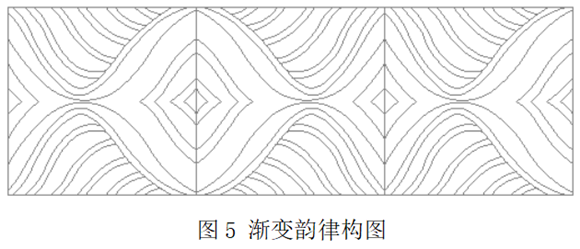
1.2韵律美
自然界中的许多事物或现象,往往由于有秩序地变化或有规律地重复出现而激起人们的美感,这种美通常称为韵律美。
例如投石入水中,激起一圈圈的水波纹,就是一种富有韵律的现象,水波纹以石落水点为中心,逐渐向外扩散形成的图案就非常有韵律感,节奏性;蜘蛛结的网,某些动物(包括昆虫)身上的斑纹,树叶的脉络也是富有韵律的图案。
产品http://www.stonebuy.com/sample/设计时有意识地模仿自然现象,可以创造出富有韵律变化和节奏感的图案,韵律美在建筑构图中的应用极为普遍。
古今中外的各种建筑,不论是单体建筑或群体建筑,乃至细部装饰,几乎处处都有应用韵律美造成节奏感。
韵律表述为下述四种:
(1)连续韵律
以一种或几种组合要素连续安排,各要素之间保持恒定的距离,可以连续地延长等,是这种韵律的主要特征。
(2)渐变韵律
重复出现的组合要素在某一方面有规律地逐渐变化,例如加长或缩短,变宽或变窄,变密或变疏,变浓或变淡等,便形成渐变的韵律。
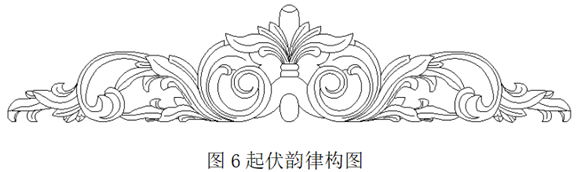
(3)起伏韵律
渐变韵律如果按照一定的规律使之变化如波浪之起伏,称为起伏韵律。
(4)交错韵律
两种以上的组合要素互相交织穿插,一隐一显,便形成交错韵律。简单的交错韵律由两种组合要素作纵横两向的交织、穿插构成:复杂的交错韵律则由三个或更多要素作多向交织、穿插构成。现代空间网架结构的构件往往具有复杂的交错韵律。
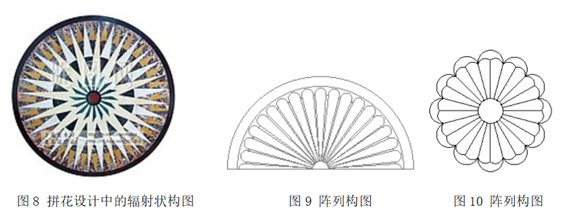
1.3辐射性原则
1.4阵列原则
以某点为中心或沿一条线将某一图形按一定距离绘制多个。图9、图10.
1.5比例原则
按比例是构图设计的一个非常重要的原则。这条原则早在几千年前就遵守,并应用到建筑实践中,尤其是柱的构图设计上更要注重。
柱的建造比例通常是:柱下径与柱高的比例是1:5.5;柱高与柱直径的比例是4或6:1。多立克柱又被称为男性柱,具“柱粗头扁,稳重凝厚”的特点。
雅典卫城的帕特农神庙即采用的是多立克柱式;爱奥尼柱总是比多立克柱要纤细:爱奥尼柱高度为8或9个直径高,在美国的改良格式中甚至更高;科林斯柱(Corinthian)比爱奥尼柱更加纤细华丽,柱高与柱身直径比例是10:1,其特色是“立体涡卷,纤巧华丽”。
黄金分割比例是物体构图设计最美的比例。
1.6工艺优化原则
1.7适用原则
1.8可装配原则
02
构图设计的方法
2.1平面构图设计
勒·柯布西耶的著名格言:“平面布局是建筑的根本”。勒·柯布西耶在《走向新建筑》中这样写道:“没有平面的那种感觉让人无法忍受,那是一种无形、空虚、混乱、任性的感觉。”
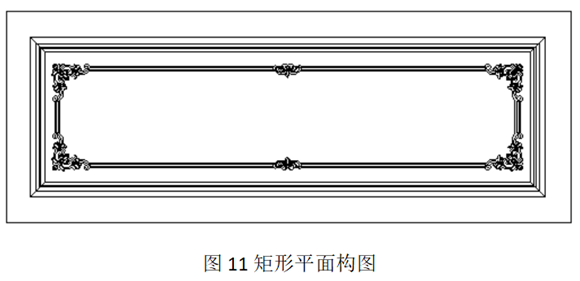
2.1.1矩形平面构图设计
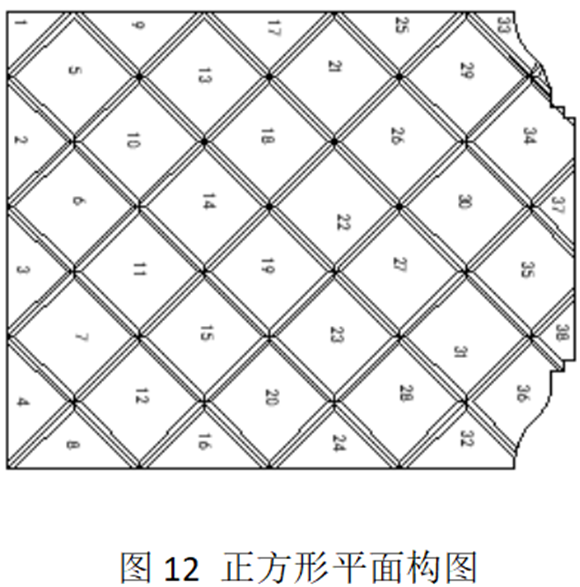
2.1.2正方形平面构图设计
2.1.3圆形平面构图设计
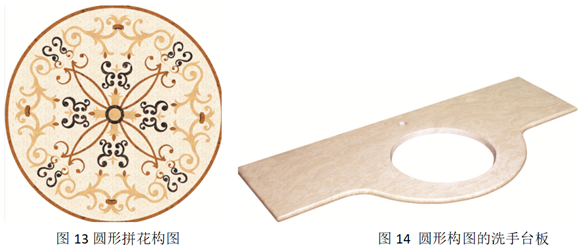
2.1.4三角形平面构图设计
2.1.5平行四边形构图设计
2.1.6椭圆形构图设计
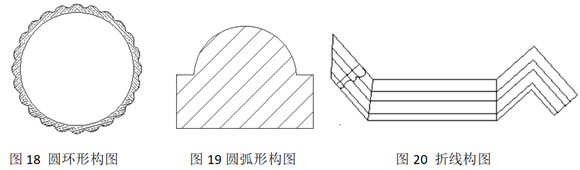
2.1.7圆环形构图设计
2.1.8圆弧形构图设计
2.1.9折线构图设计
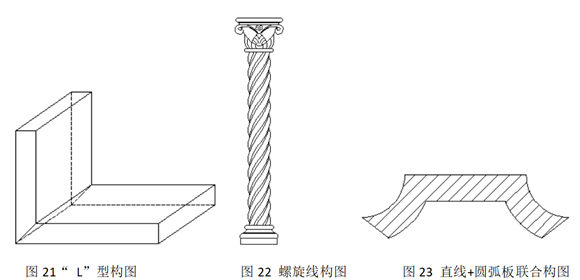
2.1.11L型构图设计设计
2.1.12螺旋线构图设计
2.1.13直线+圆弧线联合构图设计
2.1.14“回”字型构图设计
以类似中文字“回”形状构图设计。图24。
2.2构图设计中的修剪工具
以绘制图25为例阐述修剪工具“trim”的使用步骤:
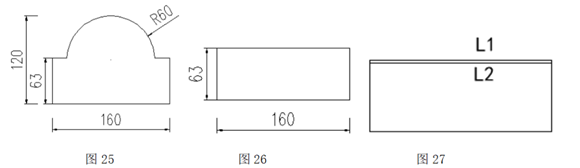
(1)绘制图26长度160mm,宽度63mm的长方形。图26;
(2)用分解命令将所绘制的长方形分解,随后用偏移(offset)命令绘制偏移3mm与L1平行的线。图27;
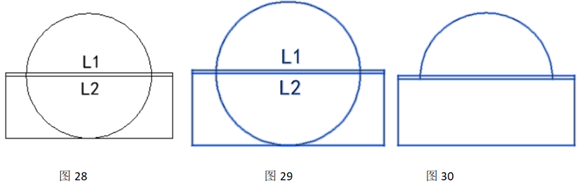
(3)以L2的中点为圆心,绘制半径60mm的圆。图28;
(4)选择修剪命令trim,随后全选所绘制图形,按回车键。图29;
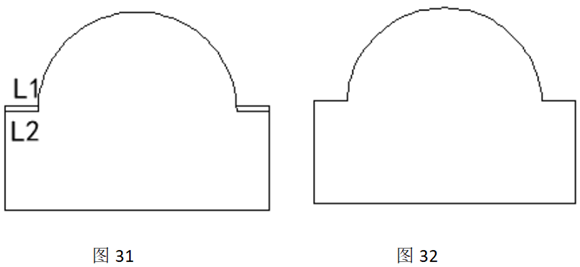
(5)选择下半段圆弧,直线L1、L2,按回车,下半段圆弧被裁剪掉,直线被裁剪掉。图30;
(6)再选择修剪命令trim,选择圆弧、直线L1,按回车键,再选择需裁剪介于L1、L2的圆弧,然后用删除命令删除L2线段剩余部分得到图32;
2.3体构图设计法
2.3.1长方体、正方体构图设计法
2.3.2圆柱体构图设计法
在同一个平面内有一条定直线和一条动线,当这个平面绕着这条定直线旋转一周时,这条动线所成的面叫做旋转面,这条定直线叫做旋转面的轴,这条动线叫做旋转面的母线。如果用垂直于轴的两个平面去截圆柱面,那么两个截面和圆柱面所围成的几何体叫做直圆柱,简称圆柱体。图34为圆柱体。
圆柱之美早在几千年之前的古希腊就被人们挖掘出来了,并被世世代代的建筑者所传承下来,至今依然闪烁着美丽的光环。
古典圆柱中流传最悠久的三种柱式多立克柱、爱奥尼柱、科林斯柱以其柱身高与柱直径和谐的比例深受历代设计师喜爱,即使到了现代,这三种柱式没有因历史的发展而被淘汰。
多立克柱式(Doric Order)是古典建筑的三种柱式中出现最早的一种(公元前7世纪)。
另外2种柱式是爱奥尼柱式和科林斯柱式,它们都源于古希腊。在希腊,多利克柱式一般都建在阶座之上,特点是柱头是个倒圆锥台,没有柱础。柱身有20条凹槽,柱头没有装饰。
2.3.3球体构图设计法
2.3.4锥体构图设计法
2.4体的建模方法
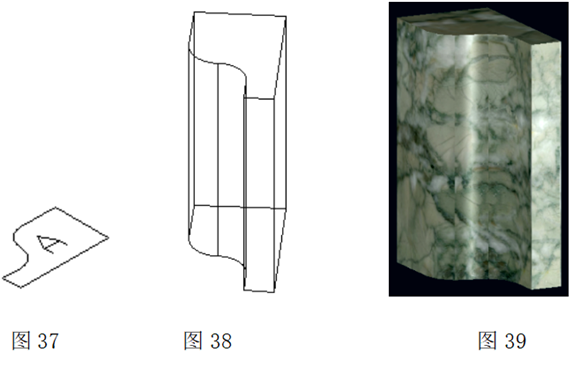
2.4.1拉伸法
图37为待拉伸的截面图;图38为截面A拉伸后形成的线条图;图39为贴材质后的渲梁效果图。
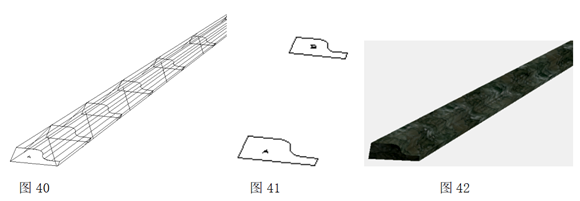
2.4.2放样法
放样 (Loft)是指通过指定一系列截面来创建新的实体或曲面的一种三维建模的方法。使用“放样”命令也要放样对象和放样路径。放样对象可以是直线、曲线、点 (仅第一个和最后一个横截面)、面域、平面等。放样路径的对象有直线、曲线、螺旋、二、三维多段线等。
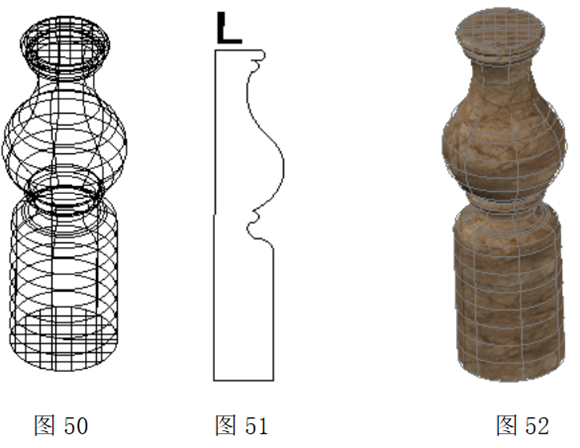
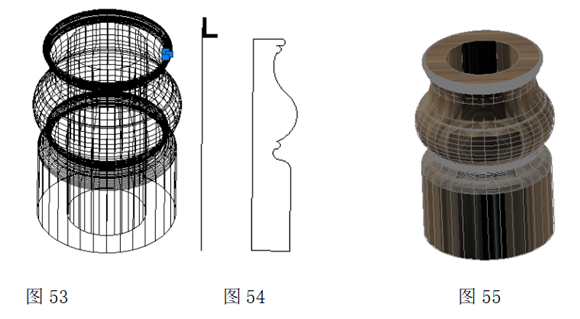
图40是用图41中的大小不同的两个截面图形A与B经过放样命令形成的线框图;图42是贴材质后的效果图。
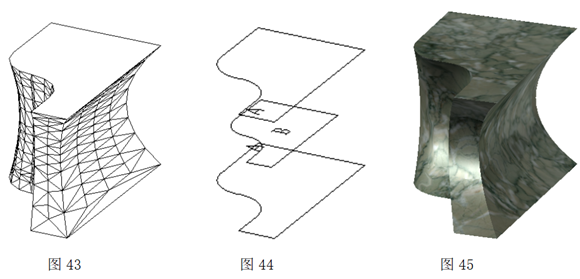
图43是用图44中3个截面放样后构成的图形,其中2个截面图A大小、形状相同,截面B比截面A小。通过放放样命令后将A与B连接成一个几何体,几何体上下两端大,中间以B为基准逐渐变小。图45为贴材质后听效果。
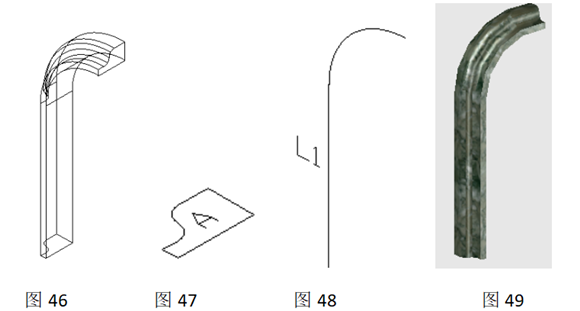
2.4.3扫掠法
扫掠 (Sweep)是通过路径扫掠二维曲线来创建三维实体或曲面的一种三维建模方法。使用“扫掠”命令需要确定扫掠对象和扫掠路径 ,而确定路径一般是造型的难点。扫掠对象是开放或封闭的 ,可以是直线 、曲线 、面域 、二维多段线等 。扫掠路径可以是直线 、二 、三维多段 线 、螺旋线 、实体或曲面的边等。
2.4.4旋转法
2.5体的布尔运算
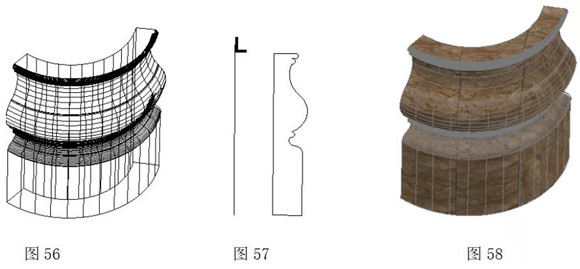
布尔运算是数学中的一个重要计算工具,对几何体通过布尔计算可以形成各种各样的物体。图59~图62是通过布尔运算中的加、减、相交运算得到的几何构图。
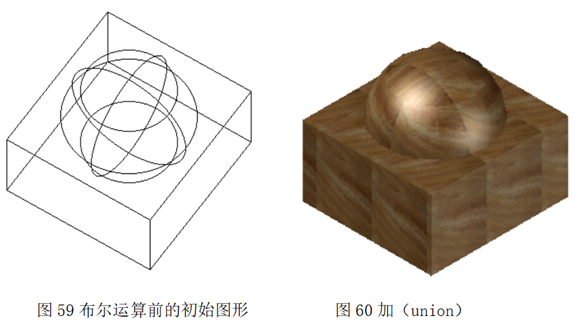

2.5.1布尔运算加法
将两个或多个几何体叠加组合在一块的运算。图63为布尔运算加法后形成的几何体。
2.5.2布尔运算减法
2.5.3布尔运行相交
对多个物体利用布尔运算的运算可以绘制出这些几何体的公共部份图形。